Isla de las Fracciones Cortadas
Pero en esta aventura no están solos, puesto que tanto nosotros como maestros y vosotros como padres, les acompañaremos en este viaje.
¡Iniciamos nuestro viaje en la ISLA DE LAS FRACCIONES CORTADAS!
_________________________________________________________________________________
Situación didáctica I: Mínimo común múltiplo, máximo común divisor y reducción de fracciones a común denominador
Objetivos de la situación:
Conocer el mínimo común múltiplo (m.c.m) y máximo común divisor (m.c.d).
Reducir fracciones a común denominador.
Conocer el mínimo común múltiplo (m.c.m) y máximo común divisor (m.c.d).
Reducir fracciones a común denominador.
Duración de la clase: 60 minutos.
Material: Regletas de Cuisenaire.
Organización del aula y metodología:
Dividimos la clase en dos partes. Los primeros 20 minutos fueron destinados a la explicación. Después, el resto de la clase, fue dedicada a la aplicación práctica de los conceptos adquiridos, en la que los alumnos trabajaron tanto en equipos, como por parejas.
Explicación teórica:
Explicación teórica:
Al llegar al aula hicimos una lluvia de ideas con nuestros alumnos acerca de qué recordábamos de las fracciones. A través de esa pregunta y este vídeo (https://www.youtube.com/watch?v=ODQpnt06M0M) realizamos una reflexión de cuándo usamos las fracciones en nuestro día a día.
A continuación, pedimos a nuestros alumnos que se pusiesen su ropaje pirata (parche, gorro…) y nos ambientamos en la historia.
En primer lugar, decimos a nuestros pequeños piratas que en esta isla no existe mejor defensa que el m.c.m:
· El número más pequeño que no es 0 y que es múltiplo de 2 o más números.
· Múltiplo: El número que se obtiene cuando lo multiplicas por otro número.
· El mínimo común múltiplo es el menor de los múltiplos comunes.
· El número más pequeño que no es 0 y que es múltiplo de 2 o más números.
· Múltiplo: El número que se obtiene cuando lo multiplicas por otro número.
· El mínimo común múltiplo es el menor de los múltiplos comunes.
Por ejemplo:
El 6 sería el mínimo común múltiplo de 2 y de 3.
Para comprobar que nuestros grumetes han comprendido el significado de mínimo común múltiplo les pedimos realizar la siguiente misión:
MISIÓN: Un grumete tiene una colección de monedas que puede agrupar de 6 en 6, de 8 en 8 y de 10 en 10, sin que falte ninguna. ¿Cuál es el menor número de monedas que puede tener?
Todos resolvieron con éxito esta misión.
En segundo lugar, les mostramos el otro gran elemento de defensa, el m.c.d, que es el mayor número que divide exactamente a dos o más números.
Los divisores de un número son aquellos que al dividir el número el resto es 0. Por ejemplo: divisores de 24 son 1, 2, 3, 4, 6, 12 y 24. Si dividimos 24 entre cualquiera de ellos el resto es 0.
El máximo común divisor de 2 o más números es el mayor de los divisores comunes a estos números. Por ejemplo: vamos a calcular el m.c.d de 30 y 42. Divisores de 30: 1, 2, 3, 5, 6, 10, 15 y 30; divisores de 42: 1, 2, 3, 6, 7, 21 y 42. Vemos que 6 es un divisor común a ambos números y es el mayor de los divisores comunes. Por lo tanto 6 es el máximo común divisor.
Para repasar y asentar estos conceptos pudimos ser partícipes de una… ¡Guerra de defensas! Dividimos a la clase en varios equipos: ROJO, VERDE, AZUL y NARANJA. Escribimos en la pizarra dos números. Tenían que encontrar cinco múltiplos de cada uno de ellos y, después, el máximo común divisor de ambos. El primer equipo capaz de defenderlo ganaría una estrella como protector de la Isla de las Fracciones Cortadas… ¡Argg!
Los números propuestos fueron los siguientes:
- Múltiplos de 3 y 5 + su m.c.d
- Múltiplos de 4 y 7 + su m.c.d
- Múltiplos de 5 y 8 + su m.c.d
- Múltiplos de 15 y 20 + su m.c.
- Múltiplos de 32 y 40 + su m.c.d
- Múltiplos de 40 y 50 + su m.c.d
Después, pedimos a un grumete voluntario que fuera valiente y saliese a la pizarra a enumerar los pasos a seguir. ¡Lo hizo genial! Escribió en la pizarra lo siguiente:
1. Escribir el m.c.m de los denominadores.
2. Poner el denominador resultante en las fracciones.
3. Cambiar también el numerador, dividiendo el denominador actual por el denominador anterior, y multiplicándolo por el antiguo numerador para encontrar el nuevo.
1. Escribir el m.c.m de los denominadores.
2. Poner el denominador resultante en las fracciones.
3. Cambiar también el numerador, dividiendo el denominador actual por el denominador anterior, y multiplicándolo por el antiguo numerador para encontrar el nuevo.
Aplicación práctica:
El concepto de m.c.m y m.c.d lo aprendimos a través de las regletas de Cuisenaire, que ellos mismos fabricaron, después de ver estos vídeos:
https://www.youtube.com/watch?v=qtohbqjBHlo (m.c.d)
Les preguntamos a los grumetes sí sabían los que eran las regletas de Cuisenaire. Uno de ellos respondió que son un juego de manipulación matemática utilizado en la escuela, así como en otros niveles de aprendizaje (idiomas). Explicamos que las regletas se pueden utilizar con niños e, incluso, con adultos, permitiendo que se comprendan mejor los números y facilitando la transición hacia el cálculo mental. Se utilizan para enseñar una amplia variedad de temas matemáticos, como las cuatro operaciones básicas, fracciones, área, volumen, raíces cuadradas, resolución de ecuaciones simples, los sistemas de ecuaciones, e incluso ecuaciones cuadráticas.
Les preguntamos a los grumetes sí sabían los que eran las regletas de Cuisenaire. Uno de ellos respondió que son un juego de manipulación matemática utilizado en la escuela, así como en otros niveles de aprendizaje (idiomas). Explicamos que las regletas se pueden utilizar con niños e, incluso, con adultos, permitiendo que se comprendan mejor los números y facilitando la transición hacia el cálculo mental. Se utilizan para enseñar una amplia variedad de temas matemáticos, como las cuatro operaciones básicas, fracciones, área, volumen, raíces cuadradas, resolución de ecuaciones simples, los sistemas de ecuaciones, e incluso ecuaciones cuadráticas.
Cuando todos construyeron sus regletas, les fuimos pidiendo por parejas que encontraran la solución de cada operación. Tras varios ejemplos, cada pareja era la que preguntaba a su compañero en lugar del docente.
Después de esta actividad, realizamos un concurso dividiendo la clase en los equipos ROJO, VERDE, AZUL y NARANJA. Proyectamos en la pizarra varias fracciones que tenían que reducir a común denominador… ¡Estuvo emocionante! Como premio a su esfuerzo, les regalamos a todos una rica piruleta pirata y finalizamos la sesión.
Comprobación del aprendizaje:
Todas estas actividades llevaban consigo la observación directa del docente. En todo momento, si se veía a un alumno algo perdido, el profesor iba a rescatarle de la terrible isla, explicándole todo aquello que necesitase, o pidiéndole a otro compañero que le explicara las dudas.
Conclusión:
Los alumnos fueron capaces de resolver todos los ejercicios sin dificultades, por lo que el objetivo de la clase se cumplió.
Los alumnos fueron capaces de resolver todos los ejercicios sin dificultades, por lo que el objetivo de la clase se cumplió.
_________________________________________________________________________________
Situación didáctica II: Equivalencia fraccionaria y expresión de fracciones como número decimal
Objetivos de la situación:
· Hallar fracciones equivalentes mediante amplificación y simplificación.
· Pasar de fracción a número decimal.
Duración de la clase: 60 minutos.
Material: Proyector, un tablero, dos dados de diferentes colores y 15 fichas por jugador, Blu-tack.
Organización del aula y metodología:
Dividimos la clase en dos partes. Los primeros 20 minutos fueron destinados a la explicación. Después, el resto de la clase fue dedicada a la aplicación práctica de los conceptos adquiridos, en la que los alumnos trabajaron tanto en equipos, como por parejas.
Explicación teórica:
El concepto de fracciones equivalentes lo explicamos de forma visual, haciendo leer a uno de nuestros grumetes esta imagen proyectada:
Imagen obtenida de: Libro de matemáticas de 6º primaria Ed. Anaya.
Profundizamos en la explicación de las fracciones equivalentes mediante su lectura y varios ejemplos:
Expresión de una fracción como número decimal:
Explicamos el concepto de equivalencia de fracciones. Además, aprovechamos para mostrarles que la división del numerador entre el denominador da como resultado el número decimal de esa fracción; así aprenden a representar las fracciones de dos formas: la fraccionaria y la decimal.
Amplificación de fracciones:
En la imagen anterior vemos cómo amplificar fracciones. Entre todos los grumetes encontramos el número por el cual se ha multiplicado cada fracción.
Simplificación de fracciones:
Utilizamos esta imagen para explicar cómo simplificar fracciones. Debemos dividir tanto numerador como denominador entre el mismo número.
Aplicación práctica:
Para el paso de fracción a número decimal dividimos a la clase por parejas y jugamos al siguiente juego:
DE FRACCIÓN A DECIMAL
2
|
0,6
|
1,5
|
4
|
6
|
0,3
|
0,6
|
0,75
|
1,3
|
0,6
|
1
|
5
|
0,5
|
0,2
|
3
|
0,25
|
0,5
|
2
|
15
|
1,6
|
0,3
|
1
|
0,5
|
1
|
1,25
|
1
|
0,8
|
0,16
|
2,5
|
2
|
1,2
|
3
|
0,4
|
1
|
0,83
|
1
|
Material necesario: Un tablero, dos dados de diferentes colores y 15 fichas por jugador.
Se debe asignar previamente los papeles a los dados; por ejemplo el dado rojo nos dará el numerador de la fracción y el dado naranja nos dará el denominador.
Reglas del juego:
- Cada jugador tira los dos dados, obteniendo con ellos una fracción. Calcula la expresión decimal de esta fracción y ocupa a continuación con una de sus fichas, una casilla del tablero que lleve esta expresión.
- Si todas las posibles casillas están ocupadas, el jugador pierde su turno.
- El juego acaba cuando un jugador consigue colocar sus 15 fichas.
GANA EL JUGADOR QUE OBTIENE LA SUMA MAYOR CON SUS CASILLAS OCUPADAS.
¡PODÉIS JUGAR EN CASA, ES DIVERTIDO!
Cuando terminaron el juego, pasamos a trabajar la equivalencia de fracciones y los conceptos amplificación y simplificación a través de quesitos. Dividimos el aula en los equipos ROJO, VERDE, AZUL y NARANJA, y les repartimos diferentes cartulinas de colores con las que tuvieron que hacer los quesitos.
Posteriormente, uno de los grupos planteaba una fracción, que los grupos restantes tenían que amplificar o simplificar, hasta conseguir llenar la pizarra de quesitos y finalizar la clase.
Comprobación del aprendizaje:
Todas estas actividades llevaban consigo la observación directa del docente. Los grumetes contaban con la ayuda de sus compañeros si les hacía falta.
Conclusión: Los alumnos fueron capaces de resolver todos los ejercicios sin dificultades, por lo que el objetivo de la sesión se superó.
_________________________________________________________________________________
Situación didáctica III: Operamos con fracciones
Objetivos de la situación:
· Sumar y restar fracciones de igual o diferente denominador.
· Multiplicar fracciones con números naturales.
Duración de la clase: 60 minutos.
Material: Fichas de dominó fraccionario, tablero de la oca.
Organización del aula y metodología:
Dividimos la clase en dos partes. Los primeros 20 minutos se dedicaron a la explicación teórica y el resto de la clase a ejercicios prácticos.
Explicación teórica:
Recordamos nuestras armas: m.c.m y m.c.d, que nos serían de gran ayuda en nuestra explicación. Nos enfrentamos a un nuevo reto: la suma y resta de fracciones con igual o diferente denominador, y multiplicación de fracciones y números enteros.
SUMA Y RESTA
Establecemos dos grupos: la suma y resta de fracciones con mismo denominador y con diferente denominador.
1. Con el mismo denominador: Únicamente dejamos el mismo denominador y operamos con los numeradores (sumar o restar). Por ejemplo:
2. Con diferente denominador: Tenemos que obtener un denominador común (m.c.m). Multiplicamos cada numerador por el número por el que acabamos de multiplicar su respectivo denominador. Por último, sumamos o restamos los numeradores obtenidos, dejando el denominador común. Por ejemplo:
mcm (3,5)= 15
para la primera fracción 15:3= 5 y 15:5=3
para la primera fracción → 5x2=10, para la segunda fracción → 4x3=12
Y ahora... tan solo quedaría operar
MULTIPLICACIÓN
Para multiplicar fracciones con números enteros seguimos los siguientes pasos:
Para practicar todo lo que acabamos de aprender, volvemos a trabajar en los equipos ROJO, VERDE, AZUL y NARANJA. ¡Otra competición de la isla!
Todos los grumetes fueron muy rápidos rellenando la ficha de actividades que se les entregó con las siguientes operaciones:
- 3/8 + 6/8 – 3/8
- 3/8 + 6/4 – 3/2
- 15/7 – 4/6
- 4x1/12
- 7x2/14
- 3x9/18
- 4/9-3/3+5/27
Así terminamos con la teoría. Ha llegado la parte más emocionante de la aventura, el afianzamiento de conceptos mediante la práctica, siempre lúdica y motivadora. ¡Vamos a verla!
Aplicación práctica:
Entregamos a cada grupo estas divertidas fichas de dominó, que tenían que lograr conectar, uniendo cada operación con su resultado.
Después de la actividad anterior, les pedimos a nuestros grumetes que se sentasen por parejas para jugar a…. ¡La temible Oca! Este era el tablero, y a continuación escribimos sus normas:
REGLAS:
Casilla fracción: Si caes en fracción… ¡De fracción a fracción y tiras porque te toca!
Casilla ¡RETO!: El maestro propone a los alumnos una operación y, el primero en resolverla, obtiene el turno para la siguiente ronda.
Casilla Anticárcel: Te salva de la cárcel.
Casilla cárcel: Dos turnos sin jugar.
Casilla del avión: Viajas de avión a avión tanto para ir hacia delante, como hacia atrás.
En las casillas con operaciones, si eran capaz de resolverlas… ¡No perdían turno!
Todas estas actividades llevaban consigo la observación directa del docente; en todo momento, si se veía a un alumno algo perdido, la profesora iba a rescatarle de la terrible isla, explicándole todo aquello que necesitase, o pidiéndole a otro compañero que ejerciese de profesor explicándole las dudas, asegurando así la comprensión del otro.
Comprobación del aprendizaje:
Todas estas actividades llevaban consigo la observación directa del docente; en todo momento, si se veía a un alumno algo perdido, la profesora iba a rescatarle de la terrible isla, explicándole todo aquello que necesitase, o pidiéndole a otro compañero que ejerciese de profesor explicándole las dudas, asegurando así la comprensión del otro.
Conclusión: Los alumnos, de nuevo, resolvieron todas las misiones sin dificultades.
_________________________________________________________________________________
Hemos aprendido muchas cosas nuevas, pero CUIDADO, aún no somos piratas experimentados y debemos recordar:
ERRORES MÁS FRECUENTES CON FRACCIONES
En este apartado explicaremos algunos errores que los alumnos cometen con mayor frecuencia. También incluimos algunos enlaces web para que podáis repasar todos juntos en casa.
1. En la equivalencia de fracciones.
A la hora de buscar una fracción equivalente a otra, ya sea por amplificación o simplificación, observamos el siguiente error:
Preguntamos al alumno si esta es una fracción equivalente.
¿Son equivalentes? → 1/3 y 3/6
Si su respuesta es sí, observamos que el niño lo ha asociado con el modelo aditivo de la suma, (+3 en este caso), al numerador y al denominador. Es decir, sumo 3 al numerador y al denominador y así sucesivamente. Esto es un error ya que para encontrar una fracción equivalente no debemos sumar, sino multiplicar o dividir el numerador y el denominador por el mismo número.
¡A través de este enlace podrás repasarlas!
2. En la suma y resta de fracciones con diferente denominador.
a) Suman y restan indiferentemente el numerador y el denominador, están acostumbrados a realizar sumas y restas con números naturales, por lo tanto, asocian el mismo procedimiento al operar con fracciones. Ejemplo:
5/9 + 3/6 = 8/15
Respuesta correcta: 57/54
b) Una vez que han aprendido que para sumar o restar con fracciones con distinto denominador, se debe encontrar el común denominador a todas, olvidan modificar el numerador para poder realizar la suma o resta en cada caso.
Ejemplo de la suma → 2/6 + 3/8 = 2/48 + 3/48 = 5/48
Respuesta correcta: 34/48
Ejemplo de la resta → 7/4 - 5/6 = 7/24 - 5/24 = 2/24
Respuesta correcta: 22/24
Revisa este enlace: ¡Te vendrá genial, grumete!
3. Al realizar multiplicaciones y divisiones.
a) Cuando el niño debe realizar una multiplicación con números fraccionarios, suelen mezclar los algoritmos de la suma, con los de la multiplicación. Es decir, busca el común denominador de cada una de las fracciones y opera. En la multiplicación no es correcto.
3/5 x 1/2 = 6/10 x 5/10 = 30/10
Respuesta correcta: 3/10
b) Por último, a la hora de dividir, observamos que operan por separado los numeradores o denominadores. Es un error frecuente. Mezclan sus conocimientos de división con números naturales y los aplica en las divisiones con fracciones.
2/6 : 1/2 = 2/2
Respuesta correcta: 4/6
_________________________________________________________________________________________



 Muy bien, grumete, has conseguido una gran victoria ante tal terrible rival pero recuerda que ahora nos queda el gran desafío de esta isla.... ¡Derrotar al pirata Barba Azul!
Muy bien, grumete, has conseguido una gran victoria ante tal terrible rival pero recuerda que ahora nos queda el gran desafío de esta isla.... ¡Derrotar al pirata Barba Azul!
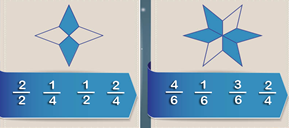
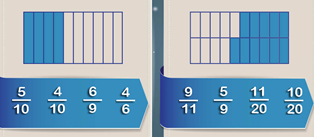
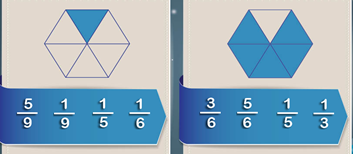
 A Luis y a mí nos han regalado un paquete con 200 caramelos cada uno. Si Luis ha comido los 4/10 del paquete y yo he comido ⅖ del paquete, ¿Cuál de los dos ha comido más?
A Luis y a mí nos han regalado un paquete con 200 caramelos cada uno. Si Luis ha comido los 4/10 del paquete y yo he comido ⅖ del paquete, ¿Cuál de los dos ha comido más?

¿Sabes cómo representaban los aztecas las fracciones?
Descúbrelo en el siguiente enlace:
MATEMAGIA: ¿Quieres sorprender a tus amigos? Te enseñamos unos fantásticos trucos que les dejarán boquiabiertos.
Para sorprender a tus amigos con los trucos de matemáticas puedes ayudarte de unos números en papelitos para elegirlos al azar sin mirar, sobres mágicos, etc. ¡Sé creativo y personaliza tu magia!
Ahora comienza la aventura… ¡Debes superar estas misiones para pasar a la siguiente isla!
MISIÓN 1: El abuelo tiene una colección de monedas que puede agrupar de 6 en 6. de 8 en 8 y de 10 en 10, sin que falte ninguna. ¿cuál es el menor número de monedas que puede tener?
MISIÓN 2: Una Piensa y resuelve.
Pequeño grumete debemos subir a nuestro navío las siguientes, pero están repartidas por diferentes partes del supermercado: 21 cajas de frutas, otras 15 cajas de bebidas y otras 28 cajas de otros alimentos, los dependientes han embalado las cosas en cajas de cartón con forma de cubo.
- Si colocan juntas las cajas frutas y de las bebidas formando un cuadrado, ¿cuántas cajas habrá en el lado de ese cuadrado? ¿Y si juntan las cajas de frutas y las de otros alimentos? ¿Y si juntan todas las cajas?
- Si deciden juntar todas las cajas y apilarlas formando un cubo, ¿cuántas cajas de altura tendrá el cubo?
MISIÓN 3: Rodea la respuesta correcta.
MISIÓN 4: Si consigues adivinar este difícil acertijo podrás abandonar la isla, pero tengo que decirte que nadie lo ha conseguido en muchísimos años...
¡ENHORABUENA!
Habéis conseguido superar las misiones, pero id con cuidado, hay otras islas más peligrosas y tendréis que emplearos a fondo para lograr vuestro objetivo.
_________________________________________________________________________________________
¡ATENCIÓN, GRUMETE, NOS LLEGAN NOTICIAS DESDE EL PUERTO!
¿Sabes cómo representaban los aztecas las fracciones?
Descúbrelo en el siguiente enlace:
¡Es muy interesante!
¡A que adivino cuánto dinero tienes en tu bolsillo y cuántos hermanos tienes!
Dile a tu amigo que revise el dinero que tiene en el bolsillo y que calcule en secreto (mentalmente) lo siguiente:
- Que multiplique esa cifra x 10
- Que le sume 25
- Que le sume el número de hermanas
- Que lo multiplique x 10
- Después que sume el número de hermanos
- Que le reste 250.
- 20€ x 10 = 200
- 200 + 25 = 225
- 225 + 1 = 226
- 226 x 10 =2.260
- 260 + 0 = 2.260
- 260 – 250 = 2.0100
Tiene 20€ en el bolsillo, 1 hermana (decenas) y 0 hermanos (unidades).
Sea cual sea el número que elijas ¡Siempre dará 12!
Pide a tu amigo que piense un número: por ejemplo, el 1.
Dile que sume 4: 1 + 4 = 5
Que reste 1: 5 – 1 = 4
Después que sume 21: 4 + 21 = 25
Que reste el número inicial: 25 – 1 =24
Divididlo entre 6: 24/6 = 4
Y multiplicadlo por 3: 4 x 3 = 12
Que reste el número inicial: 25 – 1 =24
Divididlo entre 6: 24/6 = 4
Y multiplicadlo por 3: 4 x 3 = 12
¡NOS VEMOS EN LA SIGUIENTE ISLA!
Les felicito por el blog. Ayer estuve viendo con mi hijo el tema de las fracciones y me sirvió para recordar cómo se pasaban las fracciones a números decimales y al revés porque ya lo tenía olvidado.
ResponderEliminarAsí puedo comprobar si mi hijo hace los ejercicios correctamente.
Hemos hecho el juego de la oca y lo hemos pasado muy bien en casa.
ResponderEliminarEstos juegos nos permiten compartir tiempo con nuestros hijos y además les ayudamos a estudiar sin que tengamos la sensación de estar haciéndolo por obligación.
Gracias por explicar los errores, ahora entiendo porque mi hijo se confundía al operar con fracciones.
ResponderEliminar